Why Minor Increases in Contact Resistance Matter
Connector designers understand that many variables impact contact area and how adequately the contacts do their job. This next article in the “Connector Basics” series explains why even minor increases in contact resistance matter.
 When a contact is mated, only a relatively small area is actually touching. All of the current must flow through this small area – the actual contact interface. Because the current is constricted to flow through this zone of contact, the resistance associated with this current constriction is called “constriction resistance.” Connector designers understand that many variables impact contact area (normal force, materials, surface finish, environment, etc.) and affect how adequately the contacts do their job.
When a contact is mated, only a relatively small area is actually touching. All of the current must flow through this small area – the actual contact interface. Because the current is constricted to flow through this zone of contact, the resistance associated with this current constriction is called “constriction resistance.” Connector designers understand that many variables impact contact area (normal force, materials, surface finish, environment, etc.) and affect how adequately the contacts do their job.
The overall resistance of a contact system includes elements of bulk resistance and the separable contact interface. This discussion will be targeted toward the separable interface – that portion which is subject to degradation. Bulk resistance will remain unchanged, while the resistance associated with the separable interface (constriction resistance) is subject to change – and increases with degradation.
Connector verification programs are designed to access the reliability of the contact interface – quality of the interconnection is generally based upon overall resistance measurements. The difference between the initial and final resistance measurements – the change in resistance – is generally specified, and the maximum allowed value for “passing” is defined.
The increase in constriction resistance is due to a loss of area at the contact interface; this loss may be due to, among various other mechanisms, oxide formation or perhaps a loss of normal force. Relationships that define just how much loss in area will be experienced with an increase in constriction resistance can be developed.
Developing the Relationship
In the development, Rconstriction will be the effective constriction resistance at the contact interface. Ro will be the initial constriction resistance, and Rm will be the constriction resistance at any subsequent measurement point in time. Constriction resistance is that resistance produced as a consequence of the current flow being “constricted” to the area of contact that is generated as two metallic surfaces are brought together and is given by the following equation:
Rconstriction = ρ/d
where ρ is the resistivity of the material and d is the diameter of the constriction (here simplified as a circular spot).
And so, let:
Rm = measured constriction resistance
R0 = initial constriction resistance
ΔR = increase in constriction resistance
Then at any point in time we will have: Rm = R0 + ΔR.
In terms of the diameter of the constriction at any point in time, we would have: ρ/dm = ρ/d0 + ΔR.
Finally, in terms of the increase in constriction resistance, we would have: ΔR = ρ/dm – ρ/d0, rewritten as ΔR = ρ(1/dm – 1/d0).
Suppose that the constriction resistance increases by a factor of 10 (not that uncommon with connectors that are used/tested in a corrosive environment). In other words, in this example, we would have ΔR = 9R0. In that case we would have 9R0 = ρ(1/dm – 1/d0), which simplifies down to (applying R0 = ρ/d0): d0 = 10dm.
What we have shown is that with a 10X increase in constriction resistance, we have reduced the diameter of the contact spot by a factor of 10.
The result is that with a 10X increase in constriction resistance, the final constriction diameter is 1/10 the diameter of its initial size – a significant reduction in size. And since the area of the contact spot varies as the square of the diameter, we see that the ratio of the initial area available for conduction compared to that associated with a 10X increase in constriction resistance will be but 1/100 of that value. That is, with a 10X increase in constriction resistance: A(final)/A(initial) = 1/100.
Using the previously developed relationship, it is possible to derive a general relationship between the change in contact area to the change in constriction resistance:
Afinal/Ainitial = (Rinitial/Rfinal)2
The following is a plot of the ratio of the initial to final contact area as a function of the ratio of the final to initial constriction resistance.
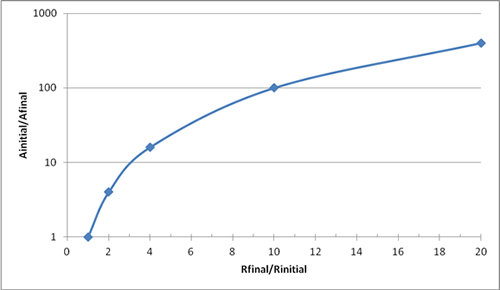
This plot demonstrates the non-linear relationship between constriction resistance and contact area. With a 10X increase in constriction resistance, the contact area decreases by a factor of 100.
For illustrative purposes, it is helpful to think of the contact spot, the constriction, in terms of wire gauge diameter. With the 10X increase in constriction resistance – assuming an initial diameter equal to that of a 12 gauge wire, we would have modified the contact spot to be resized to that of 32 gauge wire – we would be effectively taking all of the current capacity available to flow through a 12 gauge wire and require it to pass through a 32 gauge wire.
Takeaways
As effective contact area decreases, the reliability of the contact becomes questionable. The likelihood of an intermittent (or even a complete open) increases, and for the case of power contacts, the increase in temperature (due to higher constriction resistance) could potentially lead to a fire.
The overall resistance of a connector is often in the tens of milliohms. We must remember that constriction resistance is just part of the measured value, overall resistance, and for a majority of contacts, the initial constriction resistance is on the order of a milliohm or less. An increase of just a few milliohms may give the impression that the system is relatively stable, while in actuality the important parameter, constriction resistance, may have increased by several hundred percent. An increase of more than just a few milliohms could be a warning flag that demands close scrutiny. And for the case of high-current connectors, increases of a milliohm (or less) may be deemed significant.
[hr]
Ed Bock is a senior consultant at APEX Electrical Interconnection Consultants. For more than 44 years, he has worked in the connector industry (33 of those years with AMP) in the areas of contact physics, electrical contact phenomenon, fretting corrosion, contact lubrication, and wear studies (tribology). He is recognized as a prime researcher in the area of fretting corrosion, the principal failure mechanism for non-noble contact finishes (tin and tin-lead).